Multivariable Calculus 15.5 Textbook Notes

Status:

15.5 Triple Integrals in Rectangular Coordinates

The integral of a function $F(x,y,z)$ of three variables $(x,y,z)$ over a three-dimensional region $D$ is defined in a similar way by partitioning the region into small rectangles and forming the Riemann sum and taking the limit as the partition size goes to $0$.

To evaluate such an integral, we extend the Fubini Theorem to this setting by reducing it either as a single-variable integral followed by a double integral or as a three iterated single-variable integrals.

If the region $D$ can be described in terms of a two-dimensional region $R$ and two functions $f_1(x,y)\le f_2(x,y)$ in the from of $\{(x,y,z):(x,y)ϵ\mathcal{R},f_1(x,y)\le z\le f_2(x,y)\}$, then ${\iiint }_{D}F(x,y,z)dV={\iint }_{\mathcal{R}}\left({\int }_{f_1(x,y)}^{f_2(x,y)}F(x,y,z)dz\right)dA.$ The double integral is then broken down as two iterated integrals.

Example 1 is a simple example of this kind. The requirement that the region be inside $x^2+y^2+z^2=25$ and above $z=3$ gives the intersection curve as $x^2+y^2=16.$ According to our discussion, \iiint_{D}F(x,y,z)dV=\iint_{x^2+y^2\leq16}\left( \int_{3}^\sqrt{ 25-x^2-y^2 }F(x,y,z)dz \right)dA Geometrically, this corresponds to treating $D$ as the union of “thin” columns over $R$. In this case, the region $D$ can also be sliced by horizontal plates, namely, for each $z$, between $3$ and $5$, the horizontal slice is the disk $x^2+y^2\le 25-z^2$, so it is also possible to write ${\iiint }_{D}F(x,y,z)dV={\int }_3^5\left({\iint }_{x^2+y^2\le 25-z^2}F(x,y,z)dz\right)dA$ In the case of $F(x,y,z)=1$, ${\iint }_{x^2+y^2\le 25-z^2}F(x,y,z)dA=\pi (25-z^2)$ as the area of a disk of radius $\sqrt{25-z^2}$. Then ${\int }_3^5\pi (25-z^2)dz$ is easy to carry out.

Examples 2 and 3 are also simple examples of this kind. Here the same region can be described in the form of $\{(x,y,z):(x,y)ϵ{\mathcal{R}}_{xy},0\le z\le y-x\}$ (the top face of the tetrahedron has $x-y+z=0$ as its equation), and this corresponds to doing the $z$-integration first. But the region can also be described in the form $\{(x,y,z):(x,z)ϵ{\mathcal{R}}_{xz},x+z\le y\le 1\}$ over the region ${\mathcal{R}}_{xz}=\{(x,z):0\le x\le 1,0\le z\le 1-x\}$ ($z\le 1-x$ comes from the intersection of $x-y+z=0$ with the plane $y=1$; the latter is determined by the three vertices $(1,1,0),(0,1,0),(0,1,1).$)

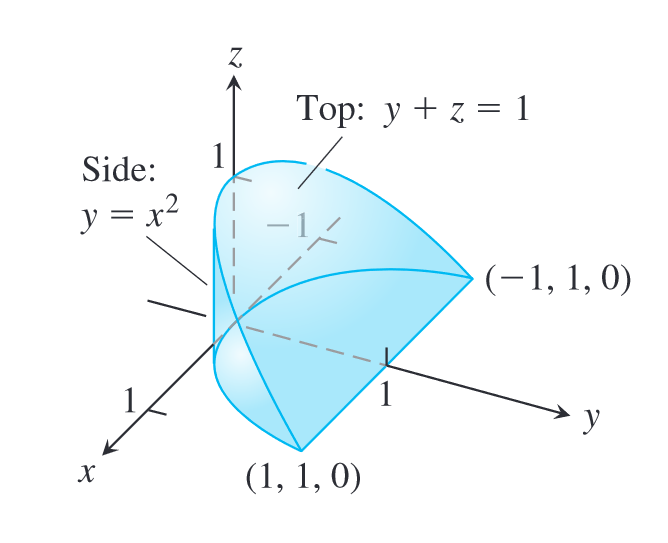
In Example 4, the easiest description of the region is in the form of $\{(x,y,z):x^2+2y^2\le 4,x^2+3y^2\le z\le 8-x^2-y^2\}$. This corresponds to doing $z$-integration first. Trying to describe such a region in the form of $\{(x,y,z):(x,z)ϵ{\mathcal{R}}_{xz},f_1(x,z)\le y\le f_2(x,z)\}$ is much harder.

There are times when its easier to break ${\iiint }_{D}F(x,y,z)dV$ in the form of ${\int }_a^b({\iint }_{{\mathcal{R}}_z}F(x,y,z)dA)dz$, where ${\mathcal{R}}_z$ is the cross-section of the region $D$ with the horizontal plane at height $z$. For example, if $D$ is enclosed by $x^2+z^2=1$ and $y^2+z^2=1$. It’s difficult to visualize the region in the form of $\{(x,y,z):(x,y)ϵ\mathcal{R},f_1(x,y)\le z\le f_2(x,y)\}$. However, the two equations $x^2+z^2=1$ and $y^2+z^2=1$ to restrict $z$ to satisfy $-1\le z\le 1$, and for each such $z$, we find $x^2\le 1-z^2$ and $y^2\le 1-z^2$, namely $|x|\le \sqrt{1-z^2}$ and $|y|\le \sqrt{1-z^2}$. This is a square of side length $\sqrt{1-z^2}$. Let’s label it as $R_z$. The volume of this region is then ${\iiint }_{D}dV={\int }_{-1}^1\left({\iint }_{{\mathcal{R}}_z}dA\right)dz={\int }_{-1}^1(1-z^2)dz.$ There are times where a triple integral is given but is difficult to evaluate directly, then one needs to figure out alternative ways of writing such a triple integrated integral. The first step is to work out the region of iteration according to the integral limits in the triple iterated integral.

Reading Questions/Quizzes

1. Let $D$ be the solid region bounded by the paraboloid $z=x^2+y^2$ and the plane $z=2y$. Write triple iterated integrals in the order $dzdxdy$ and $dzdydx$ that gives the volume of $D$. Do not evaluate either integral.
2. Here is the region of integration of the integral ${\int }_{-1}^1{\int }_{x^2}^1{\int }_0^{1-y}dzdydx.$ Rewrite the integral as an equivalent iterated integral in the order
   1. $dydzdx$
   2. $dydxdz$
   3. $dxdydz$
   4. $dxdzdy$
   5. $dzdxdy$