Multivariable Calculus 12.4 Textbook Notes

Status: Adult

Formulas

• Torque vector = $r\times F=(|r||F|\sin \theta )n$
• Magnitude of torque vector = $|r\times F|=|r||F|\sin \theta$

Find definitions/descriptions for the following terms:

• The cross product between two vectors
  • The cross product $u\times v$ (“u cross v”) is the vector $u\times v=(|u||v|\sin \theta )n$
• The right-hand rule
  • 
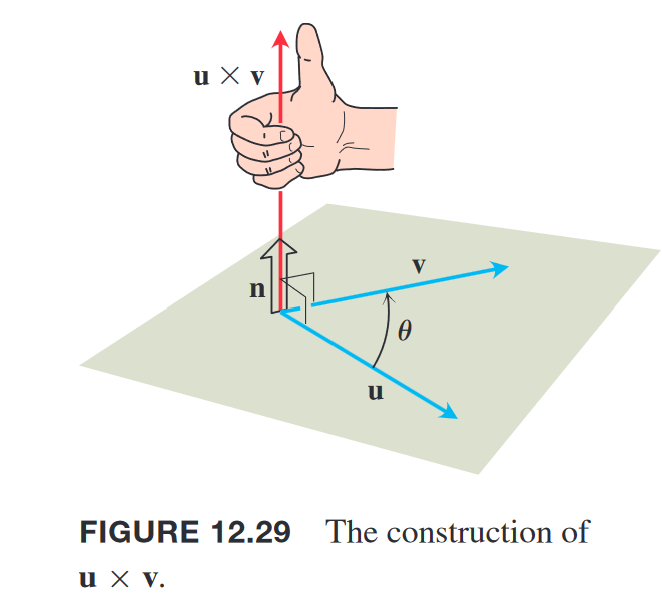
  • n is the unit normal vector that points the way your right thumb points when your fingers curl through the angle $\theta$ from u to v
• Criterion of parallel vectors in terms of their cross product
  • Nonzero vectors $u$ and $v$ are parallel if and only if $u\times v=0$
• Algebraic properties of cross product
  • $(ru)\times (sv)=(rs)(u\times v)$
  • $u\times (v+w)=u\times v+u\times w$
  • $v\times u=-(u\times v)$
  • $(v+w)\times u=v\times u+w\times u$
  • $0\times u=0$
  • $u\times (v\times w)=(u\cdot w)v-(u\cdot v)w$
• Computing u × v when u, v are taken from among the standard orthogonal vectors i, j, k.
  • TK
• Interpretation of |u × v| as the area of a certain parallelogram.
  • 
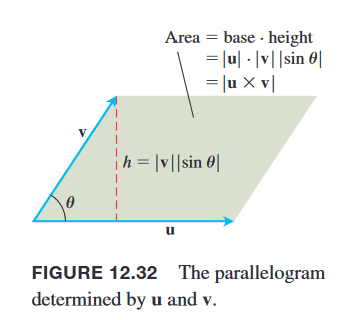
  • The magnitude of $u\times v$ is $|u\times v|=|u||v|\sin \theta$, which is the same as the area of the parallelogram defined by $u$ and $v$, with $|u|$ being the base and $|v|sin\theta$ being the height
• Determinant form for u × v.
  • If $u=u_{1}i+u_{2}j+u_{3}k$ and $v=v_{1}i+v_{2}j+v_{3}k$, then $u\times v=\left|\begin{array}{ccc}i& j& k\\ u_1& u_2& u_3\\ v_1& v_2& v_3\end{array}\right|$
• Triple scalar product (u × v) · w
  • The absolute value of this product is the volume of the parallelepiped determined by $u$, $v$, and $w$. The number $|u\times v|$ is the area of the base parallelogram. The number $|w||\cos \theta |$ is the parallelepiped’s height. Because of this geometry, $(u\times v)\cdot w$ is also called the box product of $u$, $v$, and $w$
  • Can be evaluated as a determinant: $(u\times v)\cdot w=\left|\begin{array}{ccc}{u}_1& u_2& u_3\\ v_1& v_2& v_3\\ w_1& w_2& w_3\end{array}\right|$

Reading Questions/Quizzes

• Does u × v = v × u hold?
  • No, because the two sides of the equation yield vectors that go in opposite directions
• What is u × u?
  • Since they are parallel vectors, $u\times u=0$
• Compute u × v when $u=<u_1,u_2,0>,v=<v_1,v_2,0>$.
  • $u\times v=⟨0,0,u_1{v}_2-u_2{v}_1⟩$
• Does u × (v − w) = u × v − u × w hold?
  • Yes, this is the distributive property of vector substraction
• What is (u × v) · u?
  • Since the cross product of u and v results in a vector orthogonal to both u and v, $(u\times v)\cdot u=0$
• Does it hold that (u × v) · w = (v × w) · u?
  • Yes, the scalar triple product is communitive and associative in nature
• How does (u × v) · w relate to (u × w) · v?
  • They both calculate the volume of the parallelepiped defined by vectors $u$, $v$, and $w$
• Do you see a way to define u × v when u, v are in ${\mathbb{R}}^n$ and $n\ne 3$?
  • Perhaps the determinant of an asymmetric matrix

References

Multivariable Full Textbook.pdf 12.4.pdf