Multivariable Calculus 14.4 Textbook Notes

Status:

14.4 The Chain Rule

In this section, there are a bunch of theorems each of which defines one or more chain rules. At this point, you should be asking “Wait. Chain rules? Why is there more than one?” Think back to the product rules for vector-valued functions. We had defined three different products (scalar, dot, and cross), so we had three different product rules. Similarly, there are different ways to compose functions of several variables. In single-variable calculus, we only had functions from $\mathbb{R}\mapsto \mathbb{R}$, so there was really only one type of composition. In multivariable calculus, we have already seen the chain rule for paths. That was a type of composition where $r:\mathbb{R}\mapsto {\mathbb{R}}^3$ and $r:{\mathbb{R}}^3\mapsto \mathbb{R}$, so we had $f(r):\mathbb{R}\mapsto \mathbb{R}$. In this section, we will look more closely at that chain rule, and then generalize it to other types of compositions.

Find the following definitions/concepts/formulas/theorems:

• Chain rule for paths (go back and look at this on p. 768- it’s number 7 in the box)
  • If $r(t)=x(t)i+y(t)j+z(t)k$ is a smooth path $C$, and $w=f(r(t))$ is a scalar function evaluated along $C$, then according to the Chain Rule, Theorem 6 in Section 14.4, $\frac{dw}{dt}=\frac{\partial w}{\partial x}\frac{dx}{dt}+\frac{\partial w}{\partial y}\frac{dy}{dt}+\frac{\partial w}{\partial z}\frac{dz}{dt}$
• Theorems: all of the different chain rules- see if you can figure out what they all have in common!
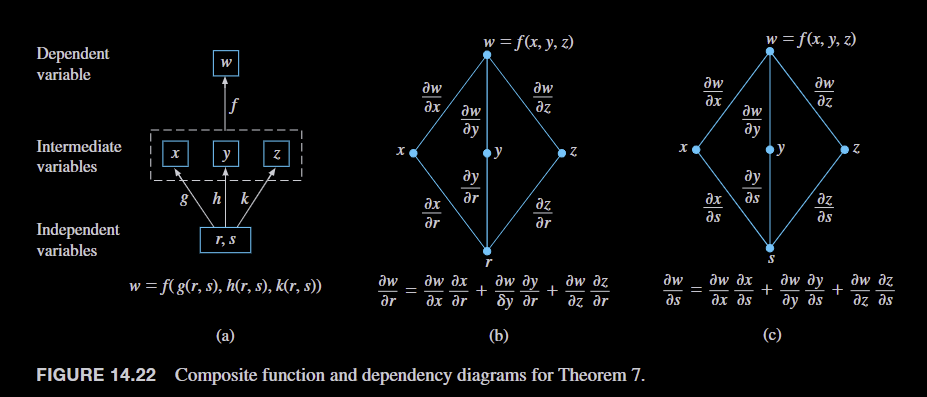
  • If $w=f(x,y)$ is differentiable and if $x=x(t),y=y(t)$ are differentiable functions of $t$, then the composition $w=f(x(t),y(t))$ is a differentiable function of $t$ and $\frac{dw}{dt}=f_x(x(t),y(t))x^{\prime }(t)+f_y(x(t),y(t))y^{\prime }(t),\text{ or }\frac{dw}{dt}=\frac{\partial f}{\partial x}\frac{dx}{dt}+\frac{\partial f}{\partial y}\frac{dy}{dt}$
  • If $w=f(x,y),x=g(r,s),\text{ and }y=h(r,s)$, then $\frac{\partial w}{\partial r}=\frac{\partial w}{\partial x}\frac{\partial x}{\partial r}+\frac{\partial w}{\partial y}\frac{\partial y}{\partial r}\text{ and }\frac{\partial w}{\partial s}=\frac{\partial w}{\partial x}\frac{\partial x}{\partial s}+\frac{\partial w}{\partial y}\frac{\partial y}{\partial s}$
• dependency diagrams (these are all in the margins, but they are very useful)
  • 
• implicit differentiation (recall that you used this in calc one for relations like $x{y}^2-y^3+x^2=3$)
  • Suppose that $F(x,y)$ is differentiable and that the equation $F(x,y)$ defines $y$ as a differentiable function of $x$. The, at any point where $F_y{\ne }_0,$ $\frac{dy}{dx}=-\frac{F_x}{F_y}$

Please work through as many of these examples as you can.

Reading Questions/Quizzes

1. Let $z=e^x\ln y,x=\ln (u\cos v),y=u\sin v$. Express $\frac{\partial z}{\partial u}$ and $\frac{\partial z}{\partial v}$ as functions of $u$ and $v$ both by using the Chain Rule and by expressing $z$ directly in terms of $u$ and $v$ before differentiating. Then (b) evaluate $\frac{\partial z}{\partial u}$ and $\frac{\partial z}{\partial v}$ at $(u,v)=\left(2,\frac{\pi }{4}\right)$.
   1. $\frac{\partial z}{\partial u}=\frac{\partial z}{\partial x}\frac{\partial x}{\partial u}+\frac{\partial z}{\partial y}\frac{\partial y}{\partial u}=\frac{e^x\ln y}{u}+\frac{e^x\sin v}{y}=\cos v\ln (u\sin v)+\cos v$
      1. $\frac{\partial z}{\partial u}{|}_{(u,v)=\left(2,\frac{\pi }{4}\right)}=\frac{\sqrt{2}}{2}\ln \sqrt{2}+\frac{\sqrt{2}}{2}$
   2. $\frac{\partial z}{\partial v}=\frac{\partial z}{\partial x}\frac{\partial x}{\partial v}+\frac{\partial z}{\partial y}\frac{\partial y}{\partial v}=-\frac{e^x\sin v\ln y}{u\cos v}+\frac{e^{x}u\cos v}{y}=-\sin v\ln (u\sin v)+\frac{u{\cos }^{2}v}{\sin v}$
      1. $\frac{\partial z}{\partial v}{|}_{(u,v)=\left(2,\frac{\pi }{4}\right)}=-\frac{\sqrt{2}}{2}\ln \sqrt{2}+\sqrt{2}$
2. Suppose that $z=f(x,y),x=u^2-v^2,y=u^2+v^2,f_x(0,2)=1\text{, and }{f}_y(0,2)=-1$. Find $\frac{\partial z}{\partial u}$ and $\frac{\partial z}{\partial v}$ at $(u,v)=(1,1)$.
   1. $\frac{\partial z}{\partial u}{|}_{(x,y)=(0,2)}=\frac{\partial z}{\partial x}{|}_{(x,y)=(0,2)}\frac{\partial x}{\partial u}{|}_{(u,v)=(1,1)}+\frac{\partial z}{\partial y}{|}_{(x,y)=(0,2)}\frac{\partial y}{\partial u}{|}_{(u,v)=(1,1)}=1\cdot 2+(-1)\cdot 2=0$
   2. TK